구현하지 않은 게 있어서 틀린 내용이 있을 수도 있습니다. 제가 구현해서 정답 받은 건 ✅로 표시했습니다.

46P/47G. Turning Red

스위치 $i$를 누른 횟수를 $x_i$라고 합시다. $x_i$는 0, 1, 2 중 하나여야 최적입니다.

각 전구가 최대 두 스위치에 연결되어 있다는 점에 주목합시다.

• 전구가 아무 스위치에도 연결되지 않았다면, 그 전구가 붉은색이면 무시합니다. 아니라면 impossible입니다.
• 전구가 스위치 1개 $i$에만 연결되었다면, $x_i$의 값이 하나로 고정됩니다.
• 전구가 스위치 2개 $i, j$에 연결되었다면, $x_i + x_j$ mod 3의 값이 하나로 고정됩니다.

스위치 1개짜리 전구로 $x_i$ 값들을 고정한 다음, 스위치 2개짜리 전구를 간선 $(i, j)$로 나타내고, 가중치를 그 고정된 $x_i + x_j$ mod 3값으로 둡시다. 이제 이분그래프 판별과 비슷한 방법으로 모든 조건에 맞는 해가 있는지 판별할 수 있습니다.

조건에 맞는 해가 있다면, 연결 요소마다 가능한 해가 최대 3개입니다. 3개의 후보 중 최적인 것을 골라서 모두 합하면 됩니다.

✅ 46Q. Doing the Container Shuffle

기댓값의 선형성에 의해

• 1을 뽑는 데 필요한 행동 수의 기댓값
• 모든 $x$에 대해, $x$를 막 뽑은 상태에서 $x+1$을 뽑는 데 필요한 행동 수의 기댓값

의 합을 구하면 됩니다. 편의상 스택에서 트럭으로 옮기는 건 제외하고, 최종 답에 $n$을 더해서 출력합시다.

1을 뽑는 데 필요한 행동 수의 기댓값은 맨 처음에 1 위에 쌓인 물건 개수의 기댓값과 같습니다. 다시 기댓값의 선형성에 의해 이 값은 (순열에서 1 뒤에 있는 물건의 개수) / 2입니다.

$x$를 막 뽑은 상태에서 $x+1$을 뽑는 데 필요한 행동 수의 기댓값은 좀 더 복잡합니다. 일반성을 잃지 않고 $x$가 맨 처음에 왼쪽 스택에 들어갔다고 합시다.

우선 순열에서 $x+1$이 $x$보다 먼저 등장하는 경우를 생각해 봅시다. 순열을 A x+1 B x C 로 나타내면 스택의 맨 처음 상태로는 다음 두 경우가 가능하고, 각각이 나올 확률은 1/2입니다.

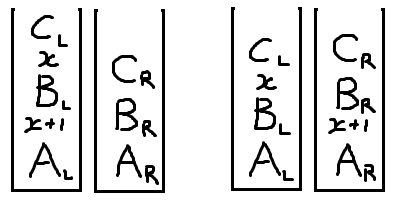
$x$를 막 뽑은 상태에서 스택의 모습은 다음과 같습니다. $C_L$이 거꾸로 써진 것은 순서가 뒤집혀 있음을 나타냅니다.

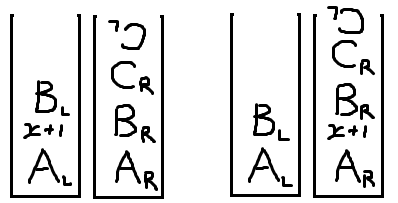
$A_L$의 크기를 $|A_L|$, 그 크기의 기댓값을 $E[|A_L|]$이라고 합시다. 그러면 $E[|A_L|] = \frac{|A|}{2}$입니다. $A_R$, $B_L$, $B_R$, $C_L$, $C_R$도 마찬가지입니다. 단, $|A|$를 구할 때는 $x$보다 큰 수만 세어야 합니다. 그보다 작은 수는 이미 제거되었기 때문입니다. 이제 왼쪽의 기댓값은 $\frac{|B|}{2}$, 오른쪽은 $\frac{|B|}{2} + |C|$이므로, 전체 기댓값은 둘의 평균인 $\frac{|B| + |C|}{2}$입니다.

순열에서 $x+1$이 $x$보다 나중에 나오는 경우도 비슷하게 풀어보면

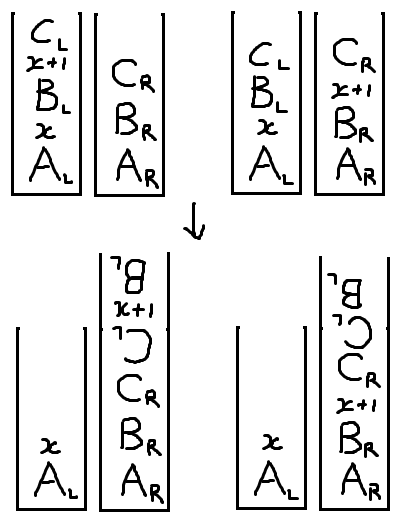
이번에도 $\frac{|B| + |C|}{2}$가 나옵니다.

이를 종합해 보면, 순열에서 $x$와 $x+1$중 먼저 나오는 쪽을 찾고, 그의 오른쪽에 있으면서 $x+1$보다 큰 수의 개수를 구해 2로 나누면 됩니다. 이 값은 펜윅 트리로 구할 수 있습니다.

46R. Zoo Management

한 번의 행동에서 사용한 간선은 vertex-disjoint cycle들을 이뤄야 합니다. 편의상 한번에 한 사이클만 고른다고 합시다. 그러면 각 행동은 “사이클을 하나 골라서 한 칸 아무 방향으로 회전시킨다“라고 할 수 있습니다.

아무 사이클에도 속하지 않는 간선, 즉 단절선은 영원히 사용할 수 없으므로 그래프에서 지워버릴 수 있습니다. 그러면 biconnected component 여러 개가 남고, 각각을 독립적으로 풀면 됩니다.

Biconnected component가 정확히 사이클 1개라면 그냥 회전만 할 수 있습니다. KMP나 해싱 등 아무 방법으로 한 수열이 다른 수열의 회전인지 판별하면 됩니다. 예를 들어 KMP를 쓴다면, “다른 수열“을 복제하고 이어 붙여서 두 배로 늘리고, 거기서 “한 수열“을 찾으면 됩니다.

Biconnected component가 사이클 2개 이상으로 이루어져 있다면, 모든 순열이 가능할 것처럼 생겼습니다. 하지만 정확히 그렇진 않습니다. 결론부터 말하면, component에 짝수 길이 사이클이 없으면 짝순열만 만들 수 있고, 아니면 모든 순열을 만들 수 있습니다. 증명은 생략하나, 사각형 두 개가 정점 하나를 공유하고 있는 그래프를 생각해보면 감이 올 수도 있습니다.

홀수 길이 사이클은 이분 그래프 판별로 풀 수 있다는 점이 잘 알려져 있는데, 짝수 길이 사이클은 어떻게 찾을까요? 짝수 길이 사이클이 없으면 component 전체가 선인장입니다. 간선을 공유하는 사이클이 2개 있다면 거기서 짝수 길이 사이클을 찾을 수 있기 때문입니다. 따라서 선인장인지 판별하고, 선인장의 각 블록 중 하나라도 짝수 길이 사이클인지 보면 됩니다.

짝순열을 써서 우리가 원하는 동물 배치를 할 수 있다는 사실은 어떻게 알 수 있을까요? 동물 번호가 중복될 수도 있어서 곤란해 보입니다. 다행히도 생각보다 간단합니다. 중복되는 동물이 있다면, 두 배치가 그냥 순열 관계인지만 확인하면 됩니다. 중복되는 동물 한 쌍을 교환하면 순열의 홀짝성이 바뀌지만 배치는 그대로니까, 어떤 배치를 만들든 홀순열과 짝순열이 모두 가능하기 때문입니다. 중복되는 동물이 없다면 평소에 하던 대로 하면 됩니다.

혹시나 해서 첨언하자면 순열의 홀짝성을 판별할 때 세그트리/펜윅트리를 쓸 필요가 전혀 없습니다. 그냥 순열을 사이클로 분할했을 때 짝수 사이클의 개수의 홀짝성이 답입니다.

✅ 46S/47J. Bridging the Gap

$N < C$이면 그냥 입력된 수의 최댓값이 답입니다. ($N = C$여도 그렇지만, 상관없습니다.) 이제 $N \geq C$라고 가정합니다. 또한 건너는 시간이 오름차순으로 정렬되어 있다고 가정합니다. 즉 $i < j$이면 사람 $i$가 $j$보다 빠르거나 같습니다.

$C = 2$의 경우 이미 BOJ에 있는 문제고, 이런 논문이 있습니다. 그 경우의 풀이를 찾고 더 큰 $C$에 대해 일반화하면 다른 논문 및 이 문제의 풀이를 얻습니다. 이 글에서는 $C = 2$일 때의 증명과 일반적인 $C$에서의 결론만 소개하고, 일반적인 $C$에서의 증명은 생략합니다.

$C = 2$라고 가정합니다. 다리를 건너가는 것을 앞 횡단, 다시 건너 돌아오는 것을 뒤 횡단, 둘을 묶어서 횡단이라고 부릅시다.

정리 1. 모든 앞 횡단의 크기가 2명, 모든 뒤 횡단의 크기가 1명인 최적해가 존재합니다.

증명. 그렇지 않은 횡단이 있다면, 그중 첫 횡단을 잡아 “문제의 횡단“이라고 합시다. 그럼 다음 4가지 케이스가 있고, 각각 더 좋은 해를 만들 수 있습니다. "" 로 감싼 것이 문제의 횡단입니다.

Case 1: "앞[x]" 뒤[x] ...
  -> ...
Case 2: ... 앞[y,z] ...<x와 y는 안 움직임>... 뒤[y] "앞[x]" ...
  -> ... 앞[x,z] ...<x와 y는 안 움직임>... ...
Case 3: ... 뒤[x] ...<x와 y는 안 움직임>... 뒤[y] "앞[x]" ...
  -> ... 뒤[y] ...<x와 y는 안 움직임>... ...
Case 4: ... 앞[x,z] ...<x는 안 움직임>... "뒤[x,y]" ...
  -> ... 앞[z] ...<x는 안 움직임>... 뒤[y] ...

■

그러한 최적해에서 앞 횡단은 $N-1$개, 뒤 횡단은 $N-2$개입니다.

정리 2. 횡단에 소요되는 전체 시간은 (모든 앞 횡단에 대해, 더 느린 사람의 시간의 합) + (모든 사람에 대해, (그 사람이 건너는 시간) * (그 사람이 앞으로 횡단한 횟수 - 1)의 합)입니다.

증명. 앞 항은 모든 앞 횡단의 시간의 합입니다. (앞으로 횡단한 횟수 - 1)은 (뒤로 횡단한 횟수)와 같고, 정리 1에 의해 모든 뒤 횡단의 크기는 1이므로, 뒤 항은 모든 뒤 횡단의 시간의 합입니다. ■

정리 2는 앞 횡단만 가지고 전체 횡단 시간을 계산할 수 있음을 의미합니다. 그렇다면 아예 뒤 횡단을 버리고, 특정 조건이 성립하는 앞 횡단만 잘 정해서 최적해를 탐색할 수 있으면 좋을 것 같습니다. 실제로 그런 데다가, 앞 횡단의 순서도 중요하지 않습니다.

정리 3. 두 명짜리 앞 횡단 $p_1q_1, \cdots, p_{N-1}q_{N-1}$이 있을 때, 각 사람이 앞 횡단 중 적어도 하나에 포함된다면, 앞 횡단의 순서가 $p_1q_1, \cdots, p_{N-1}q_{N-1}$ 의 어떤 한 순열인 올바른 횡단 순서가 존재합니다.

앞 횡단을 $pq$로 표기했는데, 이때 $p$와 $q$ 사이 대소관계는 정해두지 않았습니다. $p < q$일 수도 있고 $p > q$일 수도 있습니다.

증명. 앞 횡단을 한 번만 하는 사람을 “정착민”, 그렇지 않은 사람을 “유목민“이라고 합시다.

$N$에 대한 귀납법을 사용합니다. $N = 2$면 자명합니다.

$N \geq 3$이라고 합시다. 각 사람의 앞 횡단 횟수의 평균은 $1 < \frac{2N-2}{N} < 2$이므로, 정착민과 유목민이 적어도 한 명씩은 존재합니다. 이제

• 정착민 $x$와 유목민 $y$로 이루어진 앞 횡단 $xy$가 있다면, $xy$를 제거하고 귀납법으로 $N-1$명짜리 횡단 순서를 얻어낸 다음, 뒤 횡단 $x$, 앞 횡단 $xy$를 덧붙이면 됩니다.
• 그렇지 않다면 $N \geq 4$이고, 정착민 2명짜리 앞 횡단 $xy$와 유목민 2명짜리 앞 횡단 $zw$가 있습니다. 둘 다 제거하고 귀납법으로 $N-2$명짜리 횡단 순서를 얻어낸 다음, 뒤 횡단 $z$, 앞 횡단 $xy$, 뒤 횡단 $w$, 앞 횡단 $zw$를 덧붙이면 됩니다.

■

이제 뒤 횡단을 볼 필요가 없으니, 앞 횡단을 줄여서 그냥 “횡단“이라고 부르겠습니다. 횡단의 순서는 중요하지 않고, 조합만 찾으면 됩니다. 그중에서 구체적으로 어떤 형태가 최적인지 살펴봅시다.

직관적으로 생각해 보면, 우선 가장 빠른 사람들이 유목민 역할을 해야 할 것 같습니다. 또한 가장 오래 걸리는 사람들끼리 짝지어서 횡단해야 할 것 같고, 횡단 개수를 맞추려면 유목민을 중간에 섞어야 하는데, 유목민과 정착민이 같이 횡단해야 한다면 빠른 정착민들이랑 유목민 1이 같이 가야 할 것 같습니다. 이 성질들을 엄밀하게 정리하면 다음과 같습니다.

정리 4. 다음을 모두 만족시키는 최적해가 존재합니다.

• (1) 유목민 $x, y$에 대해 횡단 $xy$가 있을 때, 그 횡단은 $12$입니다.
• (2) 유목민 $x$와 정착민 $y$에 대해 횡단 $xy$가 있을 때, $x = 1$입니다.
• (3) 정착민 $x, y, z$에 대해 횡단 $1x$와 $yz$가 있을 때, $x < y$, $x < z$입니다.
• (4) 정착민 $x, y$에 대해 횡단 $xy$가 있을 때, $|x - y| = 1$입니다.

다른 말로 하면 $12, 12, \cdots, 12, 13, 14, \cdots, 1k, [k+1][k+2], [k+3][k+4], \cdots, [N-1]N$ 꼴의 최적해가 있습니다.

증명.

• (1) 그렇지 않다면 $12$로 바꿔도 됩니다.
• (2) 그렇지 않다면 $1y$로 바꿔도 됩니다.
• (3) 일반성을 잃지 않고 $y < z$라고 합시다. $x > y$라면 $1y$와 $xz$로 바꿔도 됩니다.
• (4) 위의 (1)(2)(3)에 의해, 정착민 2명짜리 횡단에 참여하는 사람들은 특정 $k$에 대해 $k, k+1, \cdots, N$입니다. $k$에 대한 귀납법을 거꾸로 사용합니다. $k > N$이라면 자명합니다. 횡단 $k[k+1]$이 없다면, 정착민 $x, y > k+1$에 대해 횡단 $kx$와 $ky$가 있습니다. 이를 $k[k+1]$과 $xy$로 바꿔도 됩니다. 귀납법에 의해 $k+2$ 또는 그 이후의 정착민에 대해서도 (4)가 성립합니다.

■

후보가 대략 $\frac{N}{2}$개이므로 각각의 시간을 계산하여 $O(N^2)$에 풀 수 있습니다.

위 정리들은 더 큰 $C$에 대해 다음과 같이 일반화됩니다. 증명은 생략합니다.

정리 1+. 모든 앞 횡단의 크기가 2명 이상, 모든 뒤 횡단의 크기가 1명인 최적해가 존재합니다.

정리 2+ 와 3+ 는 정리 2, 3과 거의 같습니다.

정리 4+. 다음을 모두 만족시키는 최적해가 존재합니다.

• (1&2) 횡단에 유목민이 $k$명 있을 때, 그 유목민은 $1, \cdots, k$입니다.
• (4) 각 횡단에서 정착민의 번호는 연속합니다.
• (3) 정착민이 있는 횡단을 가장 느린 사람의 시간에 대한 오름차순으로 정렬하면 유목민의 명수는 내림차순입니다.
• (보너스) 정착민이 있는 횡단 중 크기가 $C$보다 작은 것은 최대 하나이며, 그 횡단은 $1, \cdots, (횡단\ 크기)$입니다.

이제 알고리즘을 설계할 준비가 되었습니다. 맨 처음에 모든 사람들이 “색칠되지 않았다“고 하고, 추가로 횡단의 개수 조건을 맞추는 데 사용할 “빚“이라는 정수를 초기값 0으로 관리합시다.

• (1) $C$명 이하가 색칠되지 않은 상태로 남을 때까지,
  • 0 이상 $C-1$ 이하의 정수 $k$를 정합니다. $k$는 단조증가해야 합니다. - 색칠되지 않은 맨 마지막 사람을 x라고 할 때, 유목민 $1, \cdots, k$와 정착민 $x-(C-k)+1, \cdots, x$를 횡단시키고, 빚에 $1-k$를 더합니다.
• (2) 빚이 0 미만이면 실패입니다. 아니라면 색칠되지 않은 사람들을 모두 횡단시킵니다.
• (3) 빚이 0이 될 때까지,
  • 2 이상 $C$ 이하의 정수 $k$를 정합니다.
  • 유목민 $1, \cdots, k$를 횡단시키고, 빚에서 $k-1$을 뺍니다.

(1)(3)에서 $k$를 잘 정하는 게 목표입니다. DP 식을 세워보면 (색칠되지 않은 사람 수, 빚, (1)에서 마지막으로 정한 $k$값)으로 $O(N^3)$개의 상태가 생길 것처럼 생겼습니다. 하지만

• 빚이 음수인 상태는 고려할 필요가 없습니다. 빚이 감소하려면 $k>1$이어야 하는데, 그러면 단조증가 조건에 의해 빚이 매번 감소해서 0으로 못 돌아오기 때문입니다.
• 빚은 $[\frac{N}{C}]$ 이하입니다. 빚이 증가하려면 $k=0$이어야 하는데, 그럴 때마다 빚이 1 증가하고 $C$명이 색칠되기 때문입니다.
• 빚이 항상 0이상이라는 조건이 있는 한 $k$가 단조증가해야 한다는 조건은 필요가 없고, 따라서 마지막으로 정한 $k$ 값도 볼 필요가 없습니다.

그러므로 상태 $O(\frac{N^2}{C})$개에 상태 당 전이 $C$개로 총 $O(N^2)$에 문제를 풀 수 있습니다.

✅ 46T/47D. Carl’s Vacation

최적의 경로는 (1) 출발 사각뿔의 한 면을 타고 직선을 따라 바닥에 내려가고, (2) 바닥에서 도착 사각뿔의 바닥으로 직선을 따라 이동하고, (3) 도착 사각뿔의 한 면을 타고 직선을 따라 꼭대기로 올라가야 합니다.

(2)의 시작점과 도착점은 정사각형의 한 변 위에 있습니다. 변을 하나씩 선택하고, 각 변 위의 정확히 어느 지점에서 출발하고 도착할 건지를 변수 $a$와 $b$로 나타내면, (1), (2), (3)의 길이는 모두 $a$와 $b$에 대한 볼록함수입니다. 볼록함수의 합 역시 볼록함수이므로, 전체 길이도 볼록함수입니다. 따라서 삼분탐색을 이중으로 중첩해서 쓰면 됩니다.

물론 (2)에서 밑면을 뚫고 지나가면서 조건을 어기는 경우도 있겠지만, 그런 경우는 애초에 최적이 아닙니다.

✅ 46U. Toy Train Tracks

우선 직선 조각 $S$개, 커브 조각 $C$개를 다 써서 루프를 만들 수 있는지 판별해 봅시다. $S$와 $C$가 작은 경우부터 하나씩 손으로 풀어보면 규칙을 찾을 수 있습니다. 결론부터 말하면,

• $S$는 짝수여야 합니다.
• $C$는 4 이상의 짝수여야 합니다.
• $C \equiv 2 (mod\ 4)$이거나 $C = 8$일 경우, $S$는 2 이상이어야 합니다.

나머지 경우가 불가능한 이유는 후술합니다.

가능한 경우는 $C = 4$, $C = 6$, $C = 8$, $C \equiv 2 (mod\ 4)$, $C \equiv 0 (mod\ 4)$로 케이스워크를 하면 됩니다.

r---q
L---J

r----q
|r---J
LJ

rq
|L---q
|r---J
LJ

 rq
rJLq
Lq Lq
 Lq L---q
  Lqr---J
   LJ

r-q
| Lq
Lq Lq
 Lq L---q
  Lqr---J
   LJ

이제 본 문제를 풀어봅시다. 위 가능한 경우들을 정리해 보면 직선 조각을 1개 이하, 커브 조각을 7개 이하로 남기는 해가 존재하므로, $(S, C)$에 따라 최대 16개의 후보를 만들고 그중 가장 긴 것을 출력하면 됩니다.

불가능한 경우 증명:

• S가 홀수이면 불가능: 격자를 체스판으로 색칠하고, 루프를 탔을 때 각 칸에 들어오는 방향을 생각해 봅시다. 커브 조각만 사용하면 검은 칸은 항상 가로로, 흰 칸은 항상 세로로 들어옵니다. (물론 그 반대여도 됩니다.) 직선 조각을 하나 타는 순간 두 색의 역할이 바뀝니다. 즉 검은 칸은 세로로, 흰 칸은 가로로 들어오게 됩니다. 루프를 한 바퀴 돌면 두 색의 역할이 유지되어야 하므로 직선 조각은 짝수 번 타야 합니다.
• C가 홀수이면 불가능: 커브 조각을 탈 때마다 이동 방향이 가로에서 세로로, 세로에서 가로로 바뀝니다. 루프를 한 바퀴 돌면 이동 방향이 유지되어야 하므로 커브 조각은 짝수 번 타야 합니다.
• S가 0, C가 4k+2 꼴이면 불가능: 한 칸에서 커브 조각을 두 번 타면 그 칸과 대각선 방향으로 인접한 칸으로 가게 됩니다. 커브 조각 4k+2개 대신 대각선 조각 2k+1개가 있다고 생각하고 위의 C가 홀수이면 불가능 논리를 쓰면 됩니다.
• S가 0, C가 8이면 불가능: 직접 해보면 됩니다.

✅ 46V/47C. Three Kinds of Dice

편의상 1점, 0.5점이 아니라 2점, 1점씩 얻는다고 하고, 맨 마지막에 출력할 때 2로 나눕시다.

D3를 굴려서 x가 나왔을 때 내(D3)가 얻는 점수의 기댓값을 f(x)라고 하면, f는 같은 값으로 이루어진 $2n+1$개 이하의 구간으로 이루어집니다. 예를 들어 예시의 1 1 6 6 8 8과 2 4 9는

x   첫줄 다음줄
1   1/3  0
2   2/3  1/3
3   2/3  2/3
4   2/3  1
5   2/3  4/3
6   1    4/3
7   4/3  4/3
8   5/3  4/3
9   2    5/3
10  2    2
11  2    2
...

D3의 면마다 대응되는 f 값의 평균이 1 이상이면, D3는 그 주사위를 이기거나 비깁니다. 예를 들어 (2/3 + 2/3 + 2)/3 = 1.111... 이므로 두 번째 주사위가 첫 번째 주사위를 이깁니다. 이것으로 둘 중 어느 쪽이 D1이고 어느 쪽이 D2인지 알아낼 수 있습니다.

이제 우리가 D3를 만들어야 합니다. 면의 개수를 마음대로 정할 수 있으므로, 각 x에 임의의 음이 아닌 유리수 가중치를 부여할 수 있습니다. 그 대신 가중치의 합은 1이라고 합시다. 또한 x의 값 말고 (D1의 f 값, D2의 f 값) 순서쌍이 중요하고, 서로 다른 순서쌍이 $4n+1$개 이하이므로, 가중치를 부여할 대상은 그 $4n+1$개뿐입니다. 이제 우리가 구할 값은

• D1의 f 값에 대한 (가중치를 고려한) 평균이 1 이상일 때, D2의 f 값에 대한 평균의 최솟값
• D2의 f 값에 대한 평균이 1 이하일 때, D1의 f 값에 대한 평균의 최댓값

입니다.

$(x, y)$ 순서쌍 여러 개에 음이 아닌 가중치를 뒀을 때 ($x$의 평균, $y$의 평균)으로 가능한 값의 영역은, $(x, y)$들을 좌표평면에 놓았을 때 볼록 껍질의 둘레 및 내부입니다.

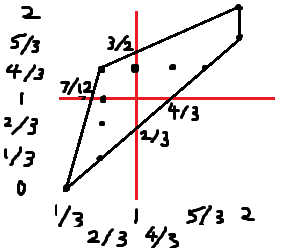
따라서 답은 그 볼록 껍질과 직선 $x = 1$의 교점, 그리고 볼록 껍질과 직선 $y = 1$의 교점입니다. 가중치에 유리수 조건이 있지만, 교점의 좌표도 유리수이므로 적절한 유리수 가중치가 항상 존재함을 알 수 있습니다. 구체적으로 어느 교점을 출력해야 되는지는 $x$, $y$ 중 어느 쪽이 D1, D2인지에 따라 적절히 정하면 됩니다.

✅ 46W/47A. Riddle of the Sphinx

• 1 0 0을 물어봅니다. 대답을 $a$라고 합시다.
• 0 1 0을 물어봅니다. 대답을 $b$라고 합시다.
• 0 0 1을 물어봅니다. 대답을 $c$라고 합시다.
• 1 1 1을 물어봅니다. 대답을 $d$라고 합시다.

만약 $a+b+c = d$라면, 스핑크스는 지금까지 참말만 했습니다. 아무거나 물어보고 대답을 들은 다음 $a$ $b$ $c$를 출력하면 됩니다.

아니라면, 스핑크스는 한 번 거짓말을 했습니다. 이 시점에서 답의 후보는

• $(a, b, c)$
• $(d-b-c, b, c)$
• $(a, d-a-c, c)$
• $(a, b, d-a-b)$

이고, 서로 다른 후보를 모두 구별하는 질의가 존재함을 증명할 수 있습니다. 스핑크스가 다음 질의에서는 참말을 할 것이므로 그걸 물어보면 됩니다.

사실 경우를 나눌 것도 없이 그냥 1 2 3을 물어봐도 됩니다.

46X. Quartets

답이 yes인지 판별할 수 있으면, no일 경우 언제부터 반칙의 존재가 확실한지도 어렵지 않게 구할 수 있습니다. 그러니 답이 yes인지 판별하는 것에 집중합시다.

예제 2를 따라가면서 풀이를 설명하면 좋을 것 같습니다. 맨 처음에 각 플레이어가 8장씩 나눠갖지만 각각이 무슨 카드인지 모르니, 다음과 같이 표기합시다. 정체를 알 수 없는 카드는 “모르는 카드”, 아니면 “아는 카드“라고 지칭합시다.

P1 [!1 !2 !3 !4 !5 !6 !7 !8]
P2 [@1 @2 @3 @4 @5 @6 @7 @8]
P3 [#1 #2 #3 #4 #5 #6 #7 #8]
P4 [$1 $2 $3 $4 $5 $6 $7 $8]

첫 기록은 1 A 2 3C no 입니다. p A q ks no 형태의 기록은 다음과 같은 정보를 제공합니다.

• 플레이어 p의 손에 k* 꼴의 카드가 있습니다. p의 손에 있는 아는 카드 중 k* 꼴이 있다면, 이는 아무 정보도 주지 않습니다. 없다면, p의 손에 있는 모르는 카드 중 하나가 k* 꼴입니다. 모르는 카드가 없다면 반칙의 존재가 확실합니다.
• 플레이어 q의 손에 ks 카드가 없습니다. q의 손에 있는 아는 카드 중에 ks가 있다면 반칙의 존재가 확실합니다. 없다면, q의 손에 있는 모르는 카드 중 아무것도 ks가 아닙니다. 모르는 카드가 없다면 아무 정보도 주지 않습니다.

다른 사람의 손으로 옮겨진 카드는 무조건 아는 카드가 되기 때문에, !1..8 + @1..3 has 3* 같이 여러 플레이어에 걸쳐서 주어지는 정보는 없습니다.

P1 [!1 !2 !3 !4 !5 !6 !7 !8] -- !1..8 has 3*
P2 [@1 @2 @3 @4 @5 @6 @7 @8] -- @1..8 hasn't 3C
P3 [#1 #2 #3 #4 #5 #6 #7 #8]
P4 [$1 $2 $3 $4 $5 $6 $7 $8]

다음 기록은 2 A 3 3A yes 입니다. p A q ks yes 형태의 기록은 다음과 같은 정보를 제공합니다.

• 플레이어 p의 손에 k* 꼴의 카드가 있습니다. 위와 같습니다.
• 플레이어 q의 손에 ks 카드가 있습니다. q의 손에 있는 아는 카드 중에 ks가 있다면 아무 정보도 주지 않습니다. 없다면, q의 손에 있는 모르는 카드 중 하나가 ks입니다. 일반성을 잃지 않고 맨 마지막 카드가 ks라고 할 수 있습니다. 모르는 카드가 없다면 반칙의 존재가 확실한데, 그런 경우가 실제로 발생할 수 있는지는 잘 모르겠습니다.

P1 [!1 !2 !3 !4 !5 !6 !7 !8] -- !1..8 has 3*
P2 [@1 @2 @3 @4 @5 @6 @7 @8 #8=3A] -- @1..8 hasn't 3C, @1..8 has 3*
P3 [#1 #2 #3 #4 #5 #6 #7]
P4 [$1 $2 $3 $4 $5 $6 $7 $8]

다음 기록은 2 A 4 3D yes 입니다. 같은 방식으로 처리합니다. 손에 이미 3A가 있으니 “3* 꼴의 카드가 있음“은 아무 정보도 주지 않습니다.

P1 [!1 !2 !3 !4 !5 !6 !7 !8] -- !1..8 has 3*
P2 [@1 @2 @3 @4 @5 @6 @7 @8 #8=3A $8=3D] -- @1..8 hasn't 3C, @1..8 has 3*
P3 [#1 #2 #3 #4 #5 #6 #7]
P4 [$1 $2 $3 $4 $5 $6 $7]

다음 기록은 2 A 1 3B no 입니다.

P1 [!1 !2 !3 !4 !5 !6 !7 !8] -- !1..8 has 3*, !1..8 hasn't 3B
P2 [@1 @2 @3 @4 @5 @6 @7 @8 #8=3A $8=3D] -- @1..8 hasn't 3C, @1..8 has 3*
P3 [#1 #2 #3 #4 #5 #6 #7]
P4 [$1 $2 $3 $4 $5 $6 $7]

다음 기록은 1 A 4 5B yes 입니다.

P1 [!1 !2 !3 !4 !5 !6 !7 !8 $7=5B] -- !1..8 has 3*, !1..8 hasn't 3B, !1..8 has 5*
P2 [@1 @2 @3 @4 @5 @6 @7 @8 #8=3A $8=3D] -- @1..8 hasn't 3C, @1..8 has 3*
P3 [#1 #2 #3 #4 #5 #6 #7]
P4 [$1 $2 $3 $4 $5 $6]

다음 기록은 1 Q 5 입니다. p Q k 형태의 기록은 플레이어 p의 손에 kA, kB, kC, kD 카드가 있다는 정보를 제공합니다. 그런데 이 플레이어의 모르는 카드에 대한 정보가 이미 있었으니, 카드를 공개하면서 이 정보도 업데이트해야 합니다.

• !1..z has k* 정보가 있는 상태에서 !z 가 ks 라는 정보를 얻었으면, 앞의 정보는 더 이상 의미가 없으므로 제거합니다. 다른 세트의 카드라는 정보를 얻었으면, !1..(z-1) has k* 로 수정합니다.
• !1..z hasn't ks 정보가 있는 상태에서 !z 가 ks 라는 정보를 얻었으면 반칙의 존재가 확실합니다. 아니라면 !1..(z-1) hasn't ks 로 수정합니다.

P1 [!1 !2 !3 !4 !5] -- !1..5 has 3*, !1..5 hasn't 3B
P2 [@1 @2 @3 @4 @5 @6 @7 @8 #8=3A $8=3D] -- @1..8 hasn't 3C, @1..8 has 3*
P3 [#1 #2 #3 #4 #5 #6 #7]
P4 [$1 $2 $3 $4 $5 $6]
quartet: (!6=5A $7=5B !7=5C !8=5D)

이제 아직 행방이 밝혀지지 않은 카드들을 모르는 카드에 잘 배정해서 모든 정보와 일치시킬 수 있는지 확인해야 합니다. 뭔가 매칭 문제를 닮았으니, 플로우 모델링을 시도해보면 다음 LR-flow 모델이 만들어집니다.

• source, sink, P1, P2, P3, P4 정점을 만듭니다.
• 각 플레이어 p 와 세트 k 의 쌍을 나타내는 pk 정점을 만듭니다. Pp 에서 pk 로 간선을 긋습니다. 용량은 4, 최소 유량은 p 에 “has k*” 정보가 있다면 1, 아니면 0으로 둡니다.
• 행방이 밝혀지지 않은 카드를 나타내는 ks 정점을 만듭니다. p 에 “hasn't ks” 정보가 없다면 pk 에서 ks 로 간선을 긋습니다. 용량은 1, 최소 유량은 0으로 둡니다.
• ks 에서 sink로 간선을 긋습니다. 용량과 최소 유량은 1로 둡니다.

이제 LR-flow 를 돌려서 해가 있는지 확인하면 됩니다.

✅ 46Y. Compression

다음 그리디 전략을 생각해볼 수 있습니다.

• 우선 연속된 같은 글자들을 하나로 합칩니다.
• 그러면 1과 0이 번갈아서 나오는 형태가 되는데, 연속된 10이나 01들을 하나로 합칩니다. 마지막에는 0, 1, 01, 10, 010, 101 중 하나가 남습니다.

이 전략은 최적입니다. 왜냐?

• 정답의 길이가 1일 필요충분조건은 “한 종류의 글자로만 이루어져 있음“입니다. 0이 하나라도 있다면 0을 전부 지울 수 없고, 1도 마찬가지이기 때문에, 0과 1이 모두 있는 문자열은 길이를 2보다 짧게 줄일 수 없습니다.
• 첫 글자를 바꿀 수 없습니다. 첫 글자를 바꾸려면 지워야 되는데, 그러면 문자열이 [abcde]abcdefgh 꼴이므로 지운 후에도 첫 글자가 유지됩니다.
• 마찬가지로 마지막 글자도 바꿀 수 없습니다.
• 01, 10, 010, 101은 (첫 글자, 마지막 글자)가 모두 다르고, 가능한 4가지 경우를 모두 커버하기 때문에, 0과 1이 모두 있는 문자열의 최종 결과는 넷 중에 정확히 하나로 정해져 있습니다.

46Z. Archaeological Recovery

TODO

✅ 47B. Schedule

먼저 주어진 $n$과 $w$에 대해 답이 유한인지 판별해 봅시다. 그러려면 길이 $n$의 이진 문자열 (편의상 1, 2가 아니라 0, 1이라고 합시다) $w$개를 만들어서 다음 조건을 만족시켜야 합니다.

인덱스 $i$에 대해, $j$번째 문자열의 $i$번째 문자가 1 인 모든 $j$의 집합을 $S_j$라고 하자. 모든 서로 다른 인덱스 $i$, $j$에 대해, (1) $S_i \cup S_j$에 없는 원소가 존재하고, (2) $S_i$와 $S_j$는 서로 부분집합 관계가 아니며, (3) $S_i \cap S_j$는 공집합이 아니어야 한다.

(1) (2) (3)은 해당 인덱스 쌍에 00, 01, 10, 11이 모두 존재함과 동치입니다.

일반성을 잃지 않고 첫 번째 문자열이 00...00 이라고 하면 (1)은 저절로 해결됩니다. (2)와 (3)이 문제인데, 방향을 바꿔서 ${1, \cdots, w}$의 부분집합 $n$개를 만든다고 합시다. 일단 (2)만 있다고 하면 슈페르너의 정리에 의해 가능한 $n$의 최댓값은 $\binom{w-1}{[\frac{w-1}{2}]}$ 입니다. 실제 해는 ${2, \cdots, w}$의 모든 $[\frac{w-1}{2}]$ 크기 부분집합을 쓰면 됩니다.

(3)이 들어가도 결론은 비슷합니다. 이 논문에 따르면 가능한 $n$의 최댓값은 $\binom{w-1}{[\frac{w-1}{2}]+1}$ 입니다. 실제 해는 ${2, \cdots, w}$의 모든 $[\frac{w-1}{2}]+1$ 크기 부분집합을 쓰면 됩니다.

이제 본 문제로 돌아갑시다. 주어진 $n$에 대해, 가능한 $n$의 최댓값이 그 이상이 되는 가장 작은 $w’$을 찾습니다. $w’ > w$라면 답은 무한입니다. $w’ \leq w$라면 답은 $w’$입니다. $w$ 대신 $w’$가 주어져도 답이 $w’$이니, 그보다 큰 $w$를 줘도 $w’$보다 작은 답을 만들 수 없기 때문입니다. 실제 해는 위에서 만든 이진 문자열 $w’$개를 돌아가면서 계속 출력하면 됩니다.

47E. A Recurring Problem

Benq 코멘트

For each continuation of length 4 up to a certain bound, count the number of recurrences with that continuation. This allows us to find the first four values of the continuation. Then, given the first four values of the continuation, we can enumerate all recurrences with that continuation, which turns out to be bounded by 4836557 for the given constraints. Though I had to spend several hours to fix the MLE / TLE / WA verdicts (the memory usage is barely under 2TB) …

arknave 코멘트

That looks largely correct. The main idea to speed up the solution and reduce its memory consumption is: for each continuation, instead of just counting the number of recurrences that begin with that continuation, compute all possible next values to this continuation, along with their frequencies. This lets you prune out a bunch of useless continuations since the values get very sparse after the first few values in the sequence.

47F. Tilting Tiles

사실 이 퍼즐에서 할 수 있는 행동은 거의 없습니다.

• 같은 방향으로 두 번 밀 이유가 없습니다. 이 퍼즐은 2048 게임이 아닙니다.
• 한 번 밀고 나서 바로 반대 방향으로 밀 이유가 없습니다. 그럼 바로 전 밀기가 의미가 없어집니다. 그래서 매번 바로 전 밀기 방향에 수직인 방향으로 밀어야 됩니다.
• 처음에 x 방향으로 밀고, 다음에 x와 수직인 y 방향으로 밀었다면, 그 다음에는 x의 반대 방향으로 밀어야 합니다. y에 수직이어야 되는데 다시 x 방향으로 미는 건 효과가 없기 때문입니다.
• 따라서 실제로 의미가 있는 행동은 소용돌이처럼 시계나 반시계 방향으로 돌아가면서 미는 것뿐입니다. 맨 처음 방향과 소용돌이의 회전 방향에 따라 총 8개의 후보가 있습니다.

이제 한 소용돌이를 잡고, 그 전략으로 우리가 원하는 배치를 만들 수 있는지 판별해 봅시다. 시작 방향과 관계없이 네 방향으로 한 번씩 미는 것을 “소용돌이 한 바퀴 돌기“라고 부릅시다.

첫 소용돌이를 돌고 나면 이후로 소용돌이 한 바퀴마다 공백의 위치가 같아짐을 증명할 수 있습니다. 예를 들어 5번 민 상태와 9번 민 상태는 각 칸에 적힌 글자는 다를 수 있어도, 각 칸이 공백인지 아닌지 여부는 같습니다.

따라서 우리가 할 일은

• 하나의 소용돌이로 치지 않고 따로 밀 횟수 $s$를 설정합니다. $0 \leq s \leq 5$ 입니다. (5도 고려해야 후술할 전략으로 모든 경우가 커버됩니다.)
• 소용돌이 방향으로 $s$번 밉니다. 공백의 위치가 우리가 원하는 배치와 다르면 실패입니다.
• 이제 공백은 됐고, 글자가 모두 맞을 때까지 소용돌이를 한 바퀴 단위로 돌립니다.

여기서 끝나면 좋겠지만, 필요한 소용돌이 횟수가 너무 커서 시간 안에 안 돌 것입니다.

소용돌이 1회는 공백이 아닌 글자들을 특정 순열에 따라 이동시키는 것으로 볼 수 있습니다. 그 순열을 얻어내려면 공백이 아닌 위치에 1, 2, 3, …을 차례대로 써넣고 소용돌이를 한 바퀴 돌리면 됩니다. 결국 우리가 풀어야 되는 문제는 다음과 같습니다.

“시작 문자열, 끝 문자열, 순열이 주어졌을 때, 순열을 반복 적용시켜 시작 문자열을 끝 문자열로 만들 수 있는가?”

순열을 사이클로 분할합니다. 그중 한 사이클의 시점에서 문제를 바라보면,

“시작 문자열, 끝 문자열이 주어졌을 때, 시작 문자열을 회전시켜 끝 문자열로 만들 수 있는가?”

단, 여기서의 시작과 끝 문자열은 그 사이클이 갖고 있는 문자들만 그 사이클 순서대로 뽑아서 만들어야 합니다. 이건 KMP나 해싱 등을 써서 풀 수 있습니다. 예를 들어 KMP를 쓴다면, 끝 문자열을 복제하고 이어 붙여서 두 배로 늘리고, 거기서 시작 문자열을 찾으면 됩니다. (어디서 들어본 말 같죠? 물론 서로 다른 대회에서 나왔습니다.)

한 사이클이라도 위 질문에 대한 답이 “아니오“라면 실패입니다. 여기서 끝나면 좋겠지만, 모든 답이 “예“여도 전체가 성공이란 보장은 없습니다. 예를 들어

abcd --> cdab
ef --> fe

위 두 경우 각각은 “예“이지만, 첫 번째 경우는 4k+2번, 두 번째 경우는 홀수 번 회전시켜야 되기 때문에, 순열을 아무리 적용해도 두 경우가 동시에 만족될 수는 없습니다. 따라서 단순히 “만들 수 있는가?“가 아니라 다음 문제를 풀어야 합니다.

“시작 문자열, 끝 문자열이 주어졌을 때, 시작 문자열을 x칸 오른쪽으로 회전시켰을 때 끝 문자열이 될 필요충분조건이 $x \equiv a (mod\ m)$이라고 하자. $a$와 $m$은 얼마인가?”

다행히도 “만들 수 있는가?“를 풀 수 있다면 위 문제도 쉽게 풀 수 있습니다. 이제 모든 사이클에 대해 모듈로 방정식 $x \equiv a (mod\ m)$을 모으고, 그 연립방정식의 해가 존재하면 성공, 아니면 실패입니다. 이제 중국인의 나머지 정리를 쓰면 됩니다. $m$의 최소공배수가 너무 클 수 있어서 정확한 해를 구하기는 어렵지만, 확장 유클리드로 해를 구하는 과정을 들여다 보면 사실 해의 존재성만 판별하는 건 gcd 하나로 충분함을 알 수 있습니다. “확장“도 지우고 그냥 유클리드 알고리즘을 쓰면 됩니다.

✅ 47H. Jet Lag

$k$초 동안 자고 일어났을 때 다음 $k$초 동안은 잘 수 없다는 조건이 거슬립니다. 이 조건이 없었다면 가능한 한 일찍 자고 늦게 일어나는 그리디 전략이 통했을 것입니다. 구체적으로,

• 첫 이벤트 이전 기간, 또는 인접한 두 이벤트 사이의 빈 기간을 “공백기“라고 합시다. 즉 타임라인은 공백기와 이벤트가 번갈아서 나열되어 있습니다.
• 첫 공백기 내내 잡니다. $k$초 동안 자면 다음 $2k$초 동안 깨어있을 수 있습니다.
• 그 다음 공백기부터는, 잤을 때 더 늦게까지 깨어있을 수 있다면 내내 자고, 아니면 건너뜁니다.
• 한 번이라도 이벤트가 끝날 때까지 깨어있을 수 없다면 불가능합니다.

다행히도 “다음 $k$초 동안은 잘 수 없다는 조건“이 들어가도 위에서 만든 전략을 조금 수정해서 재활용할 수 있습니다. 인접한 잠 스케줄이 새로운 조건에 위배되면, 둘 중 앞쪽의 스케줄을 앞당겨서 더 일찍 일어나게 바꾸면 됩니다. $k$초 동안 잘 수 없다는 조건이 없었을 때 해가 존재하지 않는다면, 조건을 추가했을 때 해도 당연히 존재하지 않습니다.

✅ 47I. Waterworld

$nm$개 조각 각각의 겉넓이를 구하고, 그 조각에 배정된 값과 곱하여 모두 합해야 됩니다.

같은 경도에 있는 조각의 겉넓이는 같습니다. 회전축을 기준으로 한 칸 만큼 돌리면 완전히 똑같은 모양이 나오기 때문입니다. 그러므로 특정 경도에 있는 조각의 겉넓이를 구하려면, 그 경도 범위로 구를 잘랐을 때 그 부분의 겉넓이를 구하고 $m$으로 나누면 됩니다.

이를 구하려면 회전체의 겉넓이 공식을 쓰면 됩니다. $t$에 대한 매개변수 곡선 $(x(t), y(t)), t \in [a, b]$를 $x$축을 중심으로 돌렸을 때 나오는 회전체의 겉넓이는 다음과 같습니다.

$2 \pi \int_a^b y(t) \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2} dt$

구체적으로, 구 $x^2 + y^2 + z^2 = r^2$를 $t_1 \leq x \leq t_2$ 범위로 잘랐을 때 그 부분의 겉넓이를 구해 봅시다. 우리가 원하는 호의 매개변수 곡선은 $(r \cos t, r \sin t), t \in [cos^{-1} \frac{x_2}{r}, cos^{-1} \frac{x_1}{r}]$입니다. 위 공식에 대입해 보면 $\sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2} = r$이므로, $A = 2 \pi r^2 \int_{t_1}^{t_2} \sin t \ dt = 2 \pi r^2 [\cos t]_{t_1}^{t_2} = 2 \pi r (x_2-x_1)$ 입니다.

그러니까, 어느 경도 범위로 자르느냐에 관계 없이 범위의 길이가 같으면 겉넓이도 같습니다. 결론적으로 모든 조각의 겉넓이가 같으므로, 그냥 입력된 수들의 평균을 출력하면 됩니다…

47K. Alea Iacta Est

$6^d$개의 상태가 있는 그래프를 생각합시다. 정점마다 어느 주사위를 고정할지를 잘 정해서, 랜덤 워크를 했을 때 도착점 중 하나에 도달하는 데 필요한 걷기 횟수의 기댓값을 최소화해야 합니다. 연립방정식을 세워서 가우스 소거 같은 걸 하기에는 어림도 없는 크기입니다.

기댓값의 근사값을 구해도 충분하고, 그 값도 작은 편이기 때문에, 모든 정점의 기댓값을 특정 초기값으로 잡고 수렴할 때까지 계산을 돌려도 될 것처럼 생겼습니다. (아마?? 월파 라이브 방송에서 들은 거긴 한데 확실하진 않습니다… TODO) 아쉽게도 이 그래프는 간선이 너무 많아서 시간 안에 수렴은 커녕 한 번 돌리기도 어렵습니다. 사실상 완전그래프입니다! 모델링을 조금 수정해서, 정점이 좀 더 많아지더라도 간선이 선형 수준으로 떨어지도록 합시다.

첫 번째 최적화는 전략과 굴리기를 분리하는 것입니다. 주사위마다 글자 6개뿐만 아니라 “곧 다시 굴릴 예정“을 의미하는 ?를 추가해 총 $7^d$개의 상태를 만듭니다. ?이 없는 상태에서는 일부 주사위를 ?로 만드는 총 $2^d$개의 간선을 추가합니다. 이 간선은 우리가 전략을 세워서 정점마다 하나씩 선택해야 합니다. 또한 ?이 있는 상태에서는 ?를 다시 굴리는 총 $6^{\text{?의 개수}}$개의 간선을 추가합니다. 이 간선은 매번 균일한 확률로 무작위로 선택됩니다. 이렇게 해도 두 번째 종류의 간선이 너무 많습니다.

두 번째 최적화는 한 번에 한 주사위만 ?로 바꾸거나 굴리는 것입니다. 즉 다음과 같이 상태를 만듭니다.

• (1) 주사위가 모두 굴려진 상태
• (2) 모두 굴려진 후, 첫 $i$개의 주사위를 ?로 바꾸거나 바꾸지 않은 상태
• (3) ?를 모두 결정한 후, 첫 $i$개의 주사위가 굴려진 상태

상태 개수는 어림잡아서 백만 단위로 나옵니다. 이제 (1)->(2)와 (2)->(2) 방향 전이의 개수는 상태 당 2개, (2)->(3) 방향 전이의 개수는 상태 당 $d$개로 상한이 잡히기 때문에, 충분히 계산을 돌릴 수 있을 만큼 간선 개수가 줄었습니다.