삼각형 찾기
6 minutes read •
단순 그래프의 정점의 개수를 $n$, 간선의 개수를 $m$이라고 합시다. 이 그래프에 있는 삼각형, 즉 길이 3의 사이클을 모두 찾을 수 있을까요?
$O(\frac{nm}{w})$
간선 하나 $uv$를 고정하고, 그 간선을 포함하는 삼각형을 찾아봅시다.
인접 행렬을 만듭니다. 그러면 $u$와 $v$에 인접한 모든 정점 $a$에 대해 삼각형 $uva$를 찾을 수 있습니다. 인접 행렬의 $u$행과 $v$행에서 둘 다 인접 표시가 된 열을 찾으면 됩니다. 시간 복잡도는 $O(nm)$입니다.
이 과정을 비트셋의 교집합 연산으로 최적화하면 시간 복잡도 $O(\frac{nm}{w})$에 모든 삼각형을 찾을 수 있습니다. 64비트 컴퓨터에서 $w = 64$입니다.
연습문제
- BOJ 20501 Facebook
- ABC258 Triangle
- BOJ 8907 네온 사인 / BOJ 8096 Monochromatic Triangles를 말그대로 붉은색, 파란색 삼각형을 직접 세서 풀 수 있습니다.
$O(m \sqrt m)$
정점 $v$의 차수를 $\deg(v)$라고 할 때, 다음 식을 생각해 봅시다.
$$\sum_{uv \in E} \min(\deg(u), \deg(v))$$
이 값은 $O(m \sqrt m)$입니다.
증명. $\sum_{v \in V} \deg(v) = 2m$이므로, $\deg(v) \geq \sqrt m$인 정점은 많아야 $O(\sqrt m)$개입니다. 그래프가 단순하므로, $\min(\deg(u), \deg(v)) \geq \sqrt m$인 간선은 많아야 $O(m)$개입니다. 나머지 간선은 $\min(\deg(u), \deg(v)) \leq \sqrt m$입니다. ■
이제 정점을 차수 순으로, 동점일 경우 번호 순으로 정렬해서 위에서 아래로 늘어놓읍시다. 위 $v$에서 아래 $p$로 가는 간선을 $v \downarrow p$라고 합시다.
모든 간선 $v \downarrow p$에 대해 간선 $pq$(위아래 상관없음)를 모두 찾을 수 있습니다. 예를 들면 아래와 같은 경우가 있습니다.
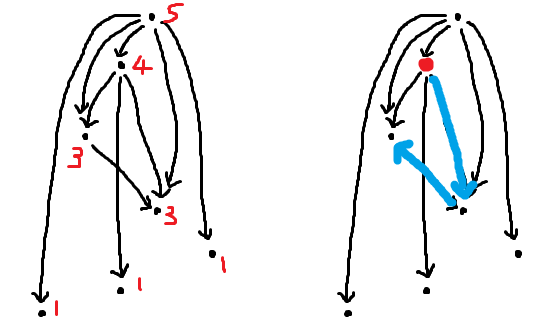
그러한 $(v, p, q)$ 쌍은 $O(\sum_{v \rightarrow p \in E} \deg(p)) = O(m \sqrt m)$개 존재합니다. $\min(\deg(v), \deg(p)) = \deg(p)$이기 때문입니다.
따라서, 위에서 아래로 가는 $v \downarrow p \downarrow q$ 꼴의 경로도 당연히 모두 찾을 수 있습니다.
이제 각 $v \downarrow p \downarrow q$에 대해 $q$와 $v$가 인접한지 확인하면 됩니다. 간단하게는 해시셋으로 구현할 수 있지만 이는 너무 무겁고, 다음과 같은 방법으로 진행할 수 있습니다.
- 우선 크기 $n$의 배열 $A$를 초기화합니다.
- 각 $v$에 대해…
- 각 간선 $v \downarrow p$에 대해 $A[p]$를 마킹합니다. 즉 $A[p]$는 “$p$가 $v$의 아래에 있으면서 인접하다“라는 뜻입니다.
- 다시 각 간선 $v \downarrow p$에 대해, 간선 $p \downarrow q$들을 순회합니다. $A[q]$가 마킹되어 있다면 삼각형 $vpq$를 찾았습니다.
- 다시 각 간선 $v \downarrow p$에 대해 $A[p]$의 마킹을 지웁니다.
각 삼각형은 $a \downarrow b \downarrow c$ 꼴의 경로를 정확히 하나씩 갖고 있으므로, 각 삼각형이 정확히 한 번씩 세어집니다. 총 시간 복잡도는 $O(m \sqrt m)$입니다. 같은 방법으로 그래프에는 삼각형이 최대 $O(m \sqrt m)$개 있음을 증명할 수 있습니다.
연습문제
- LC Enumerate Triangles
- BOJ 1762 평면그래프와 삼각형을 평면그래프 조건 없이 풀 수 있습니다.
추가 연습문제
BOJ 14571 모래시계 in $O(m \sqrt m)$
모든 삼각형을 $O(m \sqrt m)$에 찾습니다. 각 정점 $v$에 대해, $v$를 포함하는 삼각형 $vpq$에 대해 간선 $pq$의 목록을 저장해 둡니다.
모래시계의 중심 $v$를 고정하고, $v$에 대한 간선 $pq$로 이루어진 부분그래프를 생각해 봅시다. 이 부분그래프의 간선 $e$개 중 두 개를 고르되 겹치는 정점이 없도록 하는 경우의 수를 구하면 됩니다. 첫 번째 간선 $ab$를 고르고, 나머지 간선 중 $a$ 또는 $b$와 이어지는 것을 모두 제외하면, 남은 간선의 개수는 $e - \deg(a) - \deg(b) + 1$입니다. 이때 $\deg$는 부분그래프 기준입니다.
부분그래프에서 차수를 관리하는 것은 위의 $A$ 배열과 같은 방식으로 진행할 수 있습니다.
사각형의 개수
삼각형뿐만 아니라 사각형도 셀 수 있습니다! 사각형은 최대 $O(m^2)$개 있을 수 있지만, 개수는 $O(m \sqrt m)$에 구할 수 있습니다.
메인 아이디어는 아래 그림과 같습니다. 사각형을 $v \downarrow p \rightarrow q$ 꼴의 경로 두 개로 분할할 수 있으니, 그런 형태의 경로를 세는 것입니다. 각 $v \downarrow p$에 대해, $v$의 아래에 있으면서 $v$와 $p$에 인접한 정점 $q$의 개수를 $k_{vp}$라고 하면, 모든 $\frac{k_{vq}(k_{vq}-1)}{2}$의 합을 구하면 됩니다.
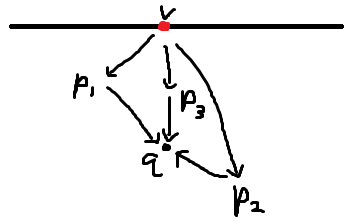
앞에서 보았듯이 $k_{vq} > 0$인 $(v, q)$는 $O(m \sqrt m)$개이고, 0보다 큰 모든 $k_{vq}$를 $O(m \sqrt m)$에 구할 수 있습니다.
위 과정을 조금 변형하면 각 정점을 포함하는 사각형의 개수도 셀 수 있습니다.
BOJ 2390 ⎐
제가 이 알고리즘을 배운 계기가 된 문제입니다. 검수하면서 풀이를 고민하다가 “사각형을 $O(M^2)$보다 빠르게 셀 수 없는데 어떻게 ⎐를 셀 수 있지?“라고 생각했는데, 사각형을 $O(M \sqrt M)$에 셀 수 있더라고요…
바로 위에서 보았듯이, 각 정점 $v$에 대해 $v$를 포함하는 사각형의 개수를 셉니다. 이제 ⎐에서 차수가 4인 정점을 “⎐의 중심“이라고 하면, 각 정점 $v$에 대해 $v$가 중심인 ⎐의 개수를 셉니다. 사각형의 개수에 $deg(v)-2$를 곱하면 됩니다.
모든 $v$에 대해 위 값을 구하고 합하면, 놀랍게도 크기 5의 완전 그래프에서 출력이 60이 나옵니다. 왜냐하면 다음 🪁 모양 케이스를 제외하지 않았기 때문입니다.
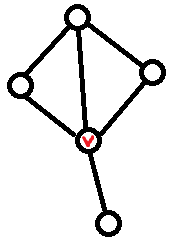
🪁를 세기 위해, 각 간선 $pq$에 대해 $pq$를 포함하는 삼각형의 개수를 셉니다. 그 후 각 간선 $pq$에 대해 $pq$가 사각형의 대각선인 🪁의 개수를 세줍니다. 삼각형의 개수를 $k$라고 할 때 $\binom{k}{2} (deg(p)-3) (deg(q)-3)$이 답입니다.
참고로 이 ⎐ 문양의 정체는 NPN open collector로, 전기회로에서 사용하는 문양입니다.
BOJ 28200 4
모든 삼각형을 찾습니다. 각 정점 $v$에 대해, $v$를 포함하는 삼각형 $vpq$에 대해 간선 $pq$의 목록을 저장해 둡니다.
한 점 $v$를 고정하고, $v$에 대한 간선 $pq$로 이루어진 부분그래프를 생각해 봅시다. 이 부분그래프에서 삼각형의 개수를 세면 되는데, 대부분의 정점에 대해서는 부분그래프가 작을 것이기 때문에 비트셋으로 풀 수 있습니다. 자세한 내용은 에디토리얼을 참조하세요.