https://acmicpc.net/problem/18796

60  +---+---+---+       +60-+60-+60-+
    |   |   |   |       10  90  80  70
20  +---+---+---+       +20-+20-+20-+
    |   |   |   |       10  90  80  70
90  +---+---+---+       +90-+90-+90-+
    10  90  80  70

예제 입력 1과 각 이동의 비용을 그림으로 나타내면 위와 같습니다. 출력은 $10 + 20 + 20 + 20 + 70 = 140$입니다.

문제의 재구성

먼저, 생각하기 쉽도록 문제를 조금 변형해 봅시다.

맨 처음에 경로 하나가 주어집니다. 이 경로는 아래로 쭉 이동한 다음 오른쪽으로 쭉 이동합니다.

60  +
    |
20  +
    |
90  +---+---+--->
    10  90  80  70

이 경로가 아래, 오른쪽 순서로 지나간 칸이 있으면 이 칸을 오른쪽, 아래 순서로 지나가도록 경로를 변경할 수 있습니다. 이때 경로의 비용도 변화하는데, 그 변화량은 인접한 두 $B_c$ 값의 차와 인접한 두 $A_r$ 값의 차를 합하여 계산할 수 있습니다.

60  +
    |
20  +---+          cost = (20-90) + (90-10)
        |               = 10
90      +---+--->
    10  90  80  70

이제 문제는 이렇게 바뀝니다.

• 격자가 있습니다. 칸 $(x, y)$를 칠하는 비용은 $Cost[x,y] := R[x] + C[y]$입니다.
• 몇 개의 칸을 색칠할 건데, 색칠한 칸은 첫 열부터 마지막 열까지 높이가 단조감소하는 히스토그램을 이루어야 합니다.
• 비용을 최소화하세요.
• 편의를 위해, 비용이 최소이더라도 칸을 더 칠하면서 비용을 유지시킬 수 있다면 최적해가 아니라고 간주합시다.

이 최소 비용을 계산한 다음, 초기 경로의 비용에 더하면 원래 문제의 답을 얻습니다.

    +---+---+---+
 40 |120|30 |30 |
    +---+---+---+
-70 |10 |-80|-80|
    +---+---+---+
     80  -10 -10

예제 입력 1을 히스토그램 버전으로 재구성하면 위와 같이 됩니다. $R$은 (-70, 40), $C$는 (80, -10, -10)입니다. 이 문제의 최적해는 아래 세 칸을 칠하는 것으로 -150의 비용이 들고, 초기 경로의 비용은 $10 \times 2 + 90 \times 3 = 290$이므로 출력은 $290 - 150 = 140$입니다.

몇 가지 관찰

우선 첫 번째 열부터 봅시다. 최적해에서 첫 번째 열의 높이가 $i$라고 합시다. 즉 $(1, 1), (2, 1), \cdots, (i, 1)$을 칠했고 $(i+1, 1)$은 칠하지 않은 상태입니다.

그러면 다음이 성립합니다.

• $Cost[i+1, 1] > 0$. 안 그러면 $(i+1, 1)$을 칠하지 않을 이유가 없습니다.
• 만약 두 번째 열이 $i$층을 칠하지 않았다면, $Cost[i, 1] \leq 0 \wedge Cost[i, 2] > 0$. 첫 번째 부등식이 성립하지 않으면 $(i, 1)$을 지우는 것이 더 좋고, 두 번째 부등식이 성립하지 않으면 $(i, 2)$를 칠하는 것이 더 좋습니다.
• 만약 두 번째 열도 $i$층을 칠했다면, $Cost[i+1,1] + Cost[i+1,2] > 0$. 안 그러면 $(i, 1)$과 $(i, 2)$를 칠하지 않는 것이 더 좋습니다.

   +---+---+---+      +---+---+---+
i+1|   |   |   |   i+1|   |   |   |
   +---+---+---+      +---+---+---+
i  |###|   |   |   i  |###|###|   |
   +---+---+---+      +---+---+---+
i-1|###|   |   |   i+1|###|###|   |
   +---+---+---+      +---+---+---+
   |###|###|   |      |###|###|   |
   +---+---+---+      +---+---+---+
    1   2              1   2

일반화

이를 일반화해봅시다. 만약 1, 2, 3, …, $k$번째 열이 정확히 $i$층까지 칠했고 $k+1$번째 열이 $i$층을 칠하지 않았다면,

• $Cost[i, 1] + \cdots + Cost[i, k] \leq 0$. 안 그러면 $(i, 1), \cdots, (i, k)$를 지우는 것이 더 좋습니다.
• $Cost[i+1, 1] + \cdots + Cost[i+1, k] > 0$. 안 그러면 $(i+1, 1), \cdots, (i+1, k)$를 칠하는 것이 더 좋습니다.

   +---+---+---+---+---+
i+1|   |   |   |   |   |
   +---+---+---+---+---+
i  |###|###|###|   |   |
   +---+---+---+---+---+
i-1|###|###|###|###|   |
   +---+---+---+---+---+
   |###|###|###|###|###|
   +---+---+---+---+---+
    1       k   k+1

그러면 무엇을 알 수 있나요?

두 부등식을 정리하면 $kR[i] + C[1] + \cdots + C[k] \leq 0 < kR[i+1] + C[1] + \cdots + C[k]$이므로, $R[i] < R[i+1]$임을 알 수 있습니다. 히스토그램을 어떻게 칠하든 위에서 제시한 $k$는 반드시 존재하므로, 이는 **최적해의 첫 번째 열이 정확히 $i$층까지 칠했다면 $R[i] < R[i+1]$**임을 의미합니다. 그리고 이 관찰은 꼭 첫 번째 열에서만 적용되는 건 아닙니다. **최적해의 어느 열이 정확히 $i$층까지 칠했을 경우, $R[i] < R[i+1]$**입니다.

반대로 말하면, $R[i] \geq R[i+1]$이면 $i$층에서 멈출 일이 없습니다. 즉 어떤 열이든 i층을 칠하면 i+1층도 반드시 칠해야 합니다.

그러므로 i층을 지웁시다

$R[i] \geq R[i+1]$이라면 $i$층과 $i+1$층을 아예 “합체“해줍시다. 즉

• 기존의 $R$ 배열이 $[R[1], \cdots, R[i], R[i+1], R[i+2], \cdots, R[N]]$이었다면,
• 새로운 $R$ 배열은 $[R[1], \cdots, R[i] + R[i+1], R[i+2], \cdots, R[N]]$이 됩니다.

그런데 이렇게 그냥 합체해 버리면 칸을 칠하는 비용이 전과 맞지 않게 됩니다. 왜냐하면 합체 전에 $(i, 1)$과 $(i+1, 1)$을 칠하는 비용은 $R[i] + R[i+1] + 2C[1]$이었는데, 합체 후에 $(i, 1)$을 칠하는 비용은 $R[i] + R[i+1] + C[1]$이기 때문입니다.

해결 방법

이를 해결하기 위해, 각 층마다 높이 값을 도입합니다. $i$층의 높이를 $H[i]$라고 할 때, $Cost[i, j] := R[i] + H[i]C[j]$로 정의하고, 두 층을 합칠 때는 $R$과 $H$ 값을 모두 합치면 됩니다.

   +---+---+---+---+---+
i  |###|###|###|   |   |
   |###|###|###|   |   |
   +---+---+---+---+---+
i-1|###|###|###|###|   |
   +---+---+---+---+---+
   |###|###|###|###|###|
   +---+---+---+---+---+
    1       k   k+1

몇 가지 관찰 v2

이제 위에서 본 그리디 전략을 다시 적용해 봅시다. 만약 1, 2, 3, …, $k$번째 열이 정확히 $i$층까지 칠했고 $k+1$번째 열이 $i$층을 칠하지 않았다면,

• $Cost[i, 1] + \cdots + Cost[i, k] = kR[i] + H[i]\mathscr{C} \leq 0$ ($\mathscr{C} := C[1] + \cdots + C[k]$).
• $Cost[i+1, 1] + \cdots + Cost[i+1, k] = kR[i+1] + H[i+1]\mathscr{C} > 0$.

따라서 $k \frac{R[i]}{H[i]} + \mathscr{C} \leq 0 < k \frac{R[i+1]}{H[i+1]} + \mathscr{C}$이므로, $\frac{R[i]}{H[i]} < \frac{R[i+1]}{H[i+1]}$입니다. 같은 이유로, $\frac{R[i]}{H[i]} \geq \frac{R[i+1]}{H[i+1]}$이면 $i$층과 $i+1$층을 합체해줄 수 있습니다.

어떻게 합체해야 하는가?

이제 우리가 할 일은 $\frac{R[i]}{H[i]} \geq \frac{R[i+1]}{H[i+1]}$인 $i$를 찾아 합체하는 과정을 이러한 $i$가 존재하지 않을 때까지 반복하는 것입니다. 그런데 이러한 $i$가 여러 개라면 무엇을 먼저 합체해야 할까요?

그 답은… 상관없습니다. 어떤 순서로 합체를 하더라도 최종적으로는 똑같은 배열이 됩니다. 왜일까요? $H$의 누적합을 $x$좌표, $R$의 누적합을 $y$좌표로 두고 점을 찍어봅시다.

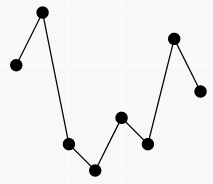
각각의 $H[i]$, $R[i]$ 쌍은 $i$번째와 $i+1$번째 점을 잇는 선분에 해당되고, 어떤 $i$에 대해 $i$번째 선분의 기울기가 $i+1$번째 선분의 기울기보다 크거나 같으면 $i+1$번째 점을 제거할 수 있습니다. 최종적으로는 선분들의 기울기가 단조증가하게 됩니다. 따라서, 어떤 순서로 합체를 하더라도 결국에는 아래로 볼록한 볼록 껍질만 남습니다.

합체 과정은 monotone chain 알고리즘처럼 스택으로 구현할 수 있습니다.

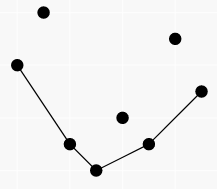
이렇게 분수를 직선의 기울기로 생각하는 발상은 이 문제, 이 문제, 이 문제 등에서도 쓸 수 있습니다.

열 합체

지금까지의 논리를 $C$에도 적용할 수 있습니다. 각 열마다 너비 $W[j]$ 값을 도입하고, $Cost[i, j] := R[i]W[j] + C[j]H[i]$로 정의한 뒤, $\frac{C[j]}{W[j]}$ 값이 단조증가하도록 열을 합쳐 줍시다.

거의 다 왔습니다!

분해

이제 아주 중요한 일이 일어납니다. 볼록 껍질의 둘레를 따라 각 $x$좌표마다 다시 점을 찍어서 볼록 껍질을 다시 $N$개의 선분으로 분해해 봅시다.

그러면 볼록 껍질은 바뀌지 않았기 때문에 최적해도 바뀌지 않습니다. 선분들의 기울기는 여전히 단조증가합니다. 그런데 이제 모든 $H[i]$가 1이기 때문에, 이는 $R[i]$가 단조증가함을 의미합니다. 마찬가지로 모든 $W[j]$가 1이면서 $C[j]$도 단조증가하도록 바꿀 수 있습니다. 답을 바꾸지 않으면서 $R$과 $C$가 단조증가한다는 매우 강력한 조건을 추가한 것입니다.

마무리

이제 나머지는 간단합니다. $Cost[i, j] > 0$이라면 $Cost[i+1, j]$와 $Cost[i, j+1]$도 모두 양수이기 때문에, $Cost[i, j] \leq 0$인 모든 $(i, j)$는 높이가 단조감소하는 히스토그램의 형태를 갖습니다. 따라서 그 히스토그램이 그냥 최적해입니다. 히스토그램 및 비용은 투 포인터와 누적합으로 찾을 수 있습니다.