BOJ 19657 Explore¶

https://www.acmicpc.net/problem/19657

풀이 미완성입니다.

테스트케이스마다 제한이 제각각이기 때문에, 각 테스트케이스를 따로 풀어야 합니다. 힌트에 나와있는 대로, 테스트케이스가 어떻게 분류되는지는 N의 값을 통해 알 수 있습니다.

테스트케이스 별 채점은 https://dmoj.ca/problem/noi19p6에서 하실 수 있습니다.

TC 1-5¶

TC1: 생략
TC2: 정점 i에 인접한 간선을 모두 찾아봅시다. modify(i)한 다음, 나머지 모든 j에 대해 query(j)가 1이면 report(i, j)를 하면 됩니다. 끝난 후에는 modify(i)를 다시 해서 되돌립시다. 이를 모든 i에 대해 수행하면 됩니다.
TC3: modify 횟수를 반으로 줄여야 합니다. 정점 i의 처리가 끝난 다음 이걸 되돌리지 말고, 모든 정점의 쿼리 값을 저장해 둡니다. 다음 정점 i+1을 처리할 때 query(j)의 값이 바뀌면 report(i+1, j)하면 됩니다.
TC4: modify를 하나 줄여야 합니다. 마지막 정점까지 왔을 때는 이미 모든 간선이 report되었을 것이기 때문에, modify(n-1)만 건너뛰면 됩니다.
TC5: query를 반으로 줄여야 합니다. 정점 i를 처리할 때, j > i인 j에 대해서만 query(j)를 하면 됩니다. j < i인 간선들은 정점 j를 처리할 때 이미 찾았을 것이기 때문입니다.

"자신 및 자신과 이웃한 정점의 레이블을 모두 바꾼다"는 생각하기 조금 어렵기 때문에, modify와 query의 정의를 살짝 바꿉시다.

modify는 자신의 레이블을 바꿉니다.
query는 자신과 이웃한 정점 중 레이블이 1인 것의 개수의 홀짝성을 반환합니다. 물론 실제로는 자신의 레이블도 포함되지만, 어차피 레이블은 modify로만 바뀌기 때문에, 모든 정점의 레이블을 저장해놓고 실제 query 값에서 빼면 됩니다.

모든 정점의 차수가 1이기 때문에, 전체 그래프는 매칭의 형태를 띱니다. 서로 이웃한 두 정점을 "매칭된다"라고 합시다.

modify와 query 개수가 O(NlogN)인 것 같이 보이므로, 분할 정복을 시도해 봅시다. 우선 0부터 N/2-1까지 전부 modify한 다음, 0부터 N-1까지 전부 query합니다. 그러면

(TODO: 밑에 부분 다시 쓰기)

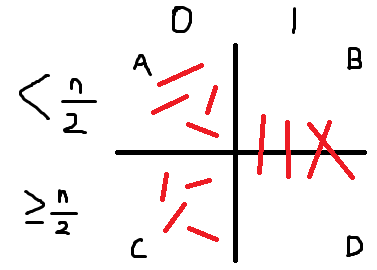
Pasted image 20220516002442.png

그러면 모든 간선은 위 그림에서 표시한 대로, (1) A의 두 점을 잇거나 (2) C의 두 점을 잇거나 (3) B의 한 점과 D의 한 점을 이어야 합니다. 왜냐?

이제 (1)과 (2)의 경우 다시 그래프가 매칭의 형태를 띠므로, 재귀적으로 A만 떼어서 풀어줍니다. 마찬가지로, 재귀적으로 C만 떼어서 풀어줍니다. A와 C는 각각 크기가 N/2 이하이기 때문에 분할 정복이 잘 됩니다.

(3)의 경우 B와 D 사이 매칭을 찾아줘야 되는데, 둘을 합치면 크기가 N/2 이하가 아닐 수도 있어서 그냥 재귀를 돌리면 안 됩니다. 여기서는 간선이 B와 D 사이를 가로지른다는 점을 활용하여 다른 방법으로 간선을 찾아줍니다.

B의 정점 중 정확히 절반을 modify하고, D의 모든 정점을 query합니다. 여기서는 modify가 B의 다른 정점들에 영향을 안 주기 때문에, B의 쿼리 값은 쿼리를 안 보내도 알 수 있습니다.

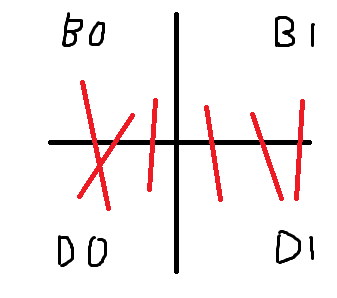
이제 정점은 쿼리 값에 따라 다시 넷으로 분류됩니다. Pasted image 20220516003912.png

간선은 B0와 D0 사이, 그리고 B1과 D1 사이에만 있기 때문에, 각각을 재귀적으로 해결하면 됩니다.

이 그래프는 루트가 0이고 자식의 번호가 부모의 번호보다 큰 트리입니다.

이번에도 O(NlogN)같이 생겼습니다. 하지만 이번에는 뒤쪽 절반만 query할 겁니다. 0부터 N/2-1까지 modify하고, N/2부터 N-1까지 query해봅시다. 그러면

그리고 번호가 N/2보다 작은 정점의 부모는 당연히 0부터 N/2-1까지 중 하나이기 때문에, 그 정점들은 전부 그룹 A에 넣을 수 있습니다.

???

???

???

???